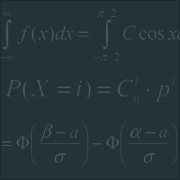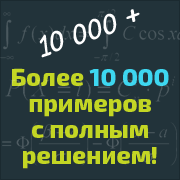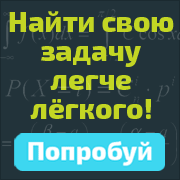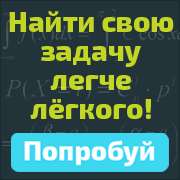Двумерная дискретная случайная величина

Ранее мы разобрали примеры решений задач для одномерной дискретной случайной величины. Но бывает, что результат испытания описывается не одной, а несколькими случайными величинами (случайным вектором).

В случае двух величин (скажем, $X$ и $Y$) мы имеем дело с так называемой двумерной дискретной случайной величиной $(X,Y)$ (или системой случайных одномерных величин). Кратко выпишем основы теории.

Система двух случайных величин: теория

Двумерная ДСВ задается законом распределения (обычно представленным в виде таблицы распределения):

$$P(X=x_i, Y=y_k)=p_{ik}, i=1,2,...,m; k=1,2,...,n; \quad \sum_{i,k}p_{ik}=1.$$

По нему можно найти одномерные законы распределения (составляющих):

$$p_i=P(X=x_i)=\sum_{k}p_{ik}, i=1,2,...,m; \\ p_k=P(Y=y_k)=\sum_{i} p_{ik}, k=1,2,...,n.$$

Интегральная функция распределения задается формулой $F(x,y)=P(X\lt x, Y\lt y)$. Даже для самого простого закона распределения 2 на 2 функция занимает 5 строк, поэтому ее редко выписывают в явном виде.

Если для любой пары возможных значений $(X=x_i, Y=y_k)$ выполняется равенство

$$P(X=x_i, Y=y_k)=P(X=x_i)\cdot P(Y=y_k),$$

то случайные величины $X, Y$ называются независимыми.

Если случайные величины зависимы, для них можно выписать условные законы распределения (для независимых они совпадают с безусловными законами):

$$P(X=x_i| Y=y_k)=\frac{P(X=x_i, Y=y_k)}{P(Y=y_k)},\\ P(Y=y_k| X=x_i)=\frac{P(X=x_i, Y=y_k)}{P(X=x_i)}.$$

Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:

$$cov (X,Y)=M(XY)-M(X)M(Y), \quad r_{XY} = \frac{cov(X,Y)}{\sqrt{D(X)D(Y)}}.$$

Далее вы найдете разные примеры задач с полным решением, где используются дискретные двумерные случайные величины (системы случайных величин).

Примеры решений

Задача 1. В продукции завода брак вследствие дефекта А составляет 10%, а вследствие дефекта В - 20%. Годная продукция составляет 75%. Пусть X - индикатор дефекта А, a Y - индикатор дефекта В. Составить матрицу распределения двумерной случайной величины (X, Y). Найти одномерные ряды распределений составляющих X и У и исследовать их зависимость.

Задача 2. Два баскетболиста по два раза бросают мяч в корзину. При каждом броске вероятность попадания для первого баскетболиста 0,6, для второго – 0,7. Случайная величина X – число попаданий первым баскетболистом по кольцу. Случайная величина Y – суммарное число попаданий обоими баскетболистами. Построить таблицу распределения случайного вектора (X,Y). Найти характеристики вектора (X,Y). Зависимы или независимы случайные величины X и Y.

Задача 3. Слово РОССИЯ разрезано по буквам. Случайным образом вынимаем две буквы, тогда X – количество гласных среди них, затем вынимаем еще две буквы и Y – количество гласных во второй паре. Составить закон распределения системы случайных величин X, Y.

Задача 4. $X, Y$ - индикаторы событий $A, B$, означающий положительные ответы соответственно на вопросы $\alpha, \beta$ социологической анкеты. По данным социологического опроса двумерная случайная величина $(X,Y)$ имеет следующую таблицу распределения.
Положительному ответу присвоен ранг 1, отрицательному – 0.
Найти коэффициент корреляции $\rho_{XY}$.

Задача 5. Составить закон распределения X - сумм очков и Y - числа тузов при выборе двух карт из колоды, содержащей только тузов, королей и дам (туз=11, дама=3, король=4)
Найти законы распределения величин Х и Y. Зависимы ли эти величины? Написать функцию распределения для (Х, Y). Построить ковариационный граф. Посчитать ковариацию (X,Y). Написать ковариационную матрицу. Посчитать корреляцию (X,Y) и написать корреляционную матрицу.

Задача 6. Бросаются две одинаковые игральные кости. Случайная величина X равна 1, если сумма выпавших чисел четна, и равна 0 в противном случае. Случайная величина Y равна 1, если произведение выпавших чисел четно, и 0 в противном случае. Описать закон распределения случайного вектора (X,Y). Найти D[X], D[Y] и cov[X,Y].

Задача 7. В урне лежат 100 шаров, из них 25 белых. Из урны последовательно вынимают два шара. Пусть $X_i$ – число белых шаров, появившихся при $i$-м вынимании. Найти коэффициент корреляции между величинами $X_1$ и $X_2$.

Задача 8. Для заданного закона распределения вероятностей двухмерной случайной величины (Х, Y):
Y\X 2 5
8 0,15 0,10
10 0,22 0,23
12 0,10 0,20
Найти коэффициент корреляции между величинами Х и Y.

Задача 9. Задана дискретная двумерная случайная величина (X,Y).
А) найти безусловные законы распределения составляющих;
Б) построить регрессию случайной величины Y на X;
В) построить регрессию случайной величины X на Y;
Г) найти коэффициент ковариации;
Д) найти коэффициент корреляции.
20 30 40 50 70
3 0,01 0,01 0,02 0,02 0,01
4 0,04 0,3 0,06 0,03 0,01
5 0,02 0,03 0,06 0,07 0,05
9 0,05 0,03 0,04 0,02 0,03
10 0,03 0,02 0,01 0,01 0,02

Задача 10. Система (x, y) задана следующей двумерной таблицей распределения вероятностей. Определить:
А) безусловные законы распределения составляющих;
Б) условный закон распределения y при x=1;
В) условное математическое ожидание x при y=2.
Г) вероятность того, что случайная величина (x,y) будет принадлежать области $|x|+|y|\le 3$.
-3 0 2
-1 0 0,1 0,15
1 0,05 0,3 0,05
2 0,15 0,05 0,15

Решебник по теории вероятности онлайн

Больше 16000 решенных и оформленных задач по теории вероятности: