Основные формулы комбинаторики

Учитесь решать задачи по комбинаторике? На самом начальном этапе нужно изучить основные формулы комбинаторики: сочетания, размещения, перестановки (смотрите подробнее ниже) и научиться их применять для решения задач.

Как выбрать формулу комбинаторики?

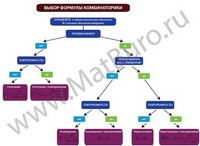
Мы подготовили для вас наглядную схему с примерами решений по каждой формуле комбинаторики:

• алгоритм выбора формулы (сочетания, перестановки, размещения с повторениями и без),
• рекомендации по изучению комбинаторики,
• 6 задач с решениями и комментариями на каждую формулу.

Перестановки

Пусть имеется $n$ различных объектов.
Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

$$P_n=n!=1\cdot 2\cdot 3 \cdot ... \cdot (n-1) \cdot n$$

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.

Пример всех перестановок из $n=3$ объектов (различных фигур) - на картинке справа. Согласно формуле, их должно быть ровно $P_3=3!=1\cdot 2\cdot 3 =6$, так и получается.

С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов - уже 3628800 (больше 3 миллионов!).

Еще: онлайн калькулятор перестановок.

Размещения

Пусть имеется $n$ различных объектов.
Будем выбирать из них $m$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $m$, а их число равно

$$A_n^m=\frac{n!}{(n-m)!}=n\cdot (n-1)\cdot ... \cdot (n-m+1)$$

Пример всех размещений из $n=3$ объектов (различных фигур) по $m=2$ - на картинке справа. Согласно формуле, их должно быть ровно $A_3^2=3\cdot (3-2+1)=3\cdot 2 =6$.

Вычисляем на лету: онлайн калькулятор размещений.

Сочетания

Пусть имеется $n$ различных объектов.
Будем выбирать из них $m$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $m$, а их число равно

$$C_n^m=\frac{n!}{(n-m)!\cdot m!}$$

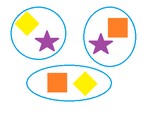
Пример всех сочетаний из $n=3$ объектов (различных фигур) по $m=2$ - на картинке справа. Согласно формуле, их должно быть ровно $C_3^2=\frac{3!}{(3-2)!\cdot 2!} =3$. Ясно, что сочетаний всегда меньше чем размещений (так как при размещениях порядок важен, а для сочетаний - нет), причем именно в $m!$ раз, то есть верна формула связи:

$$A_n^m = C_n^m \cdot P_m.$$

Удобный и бесплатный онлайн калькулятор сочетаний.

Решебник задач по комбинаторике

Изучаем комбинаторику: полезные ссылки

Видеоуроки по комбинаторике Онлайн учебник: Элементы комбинаторики Примеры решений

Как решать задачи по комбинаторике? Формулы комбинаторики с примерами Решение на заказ