Формула Бернулли в Excel

В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи - решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!

Схема независимых испытаний

В общем виде схема повторных независимых испытаний записывается в виде задачи:

Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) - соответственно $q=1-p$. Найти вероятность $P_n(k)$, что событие $A$ наступит в точности $k$ раз в $n$ опытах.

Эта вероятность вычисляется по формуле Бернулли:

$$P_n(k)=C_n^k \cdot p^k \cdot (1-p)^{n-k}=C_n^k \cdot p^k \cdot q^{n-k}. \qquad(1)$$

Здесь $C_n^k$ - число сочетаний из $n$ по $k$.

Еще: онлайн калькуляторы для формулы Бернулли.

Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:

• Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
• Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
• События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.

Если эти условия выполнены - мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет - ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.

Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.

Формула Бернулли в Эксель

Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП(), выдающая определенную вероятность биномиального распределения.

Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0).

Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).

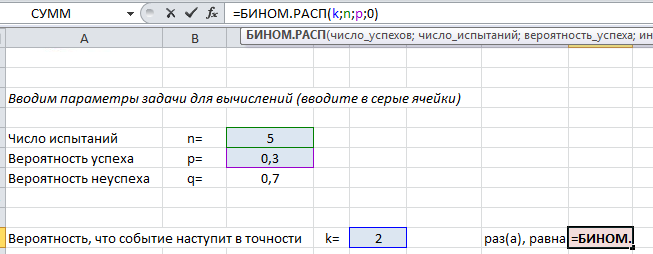
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:

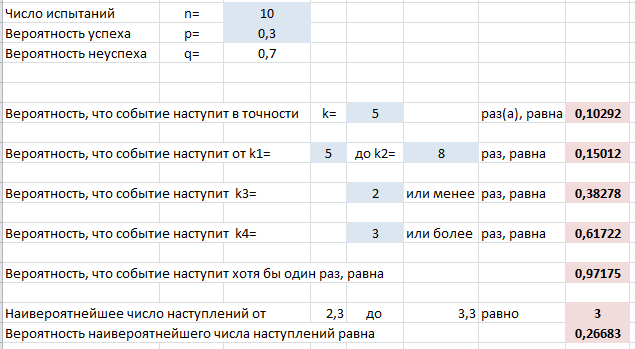
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):

• Событие произойдет в точности $k$ раз из $n$:
  =БИНОМ.РАСП(k;n;p;0)
  $$P_n(k)=C_n^k \cdot p^k \cdot q^{n-k}$$
• Событие произойдет от $k_1$ до $k_2$ раз:
  =БИНОМ.РАСП(k_2;n;p;1) - БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
  $$P_n(k_1\le X \le k_2)=\sum_{i=k_1}^{k_2} C_n^i \cdot p^i \cdot q^{n-i}$$
• Событие произойдет не более $k_3$ раз:
  =БИНОМ.РАСП(k_3;n;p;1)
  $$P_n(0\le X \le k_3)=\sum_{i=0}^{k_3} C_n^i \cdot p^i \cdot q^{n-i}$$
• Событие произойдет не менее $k_4$ раз:
  =1 - БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
  $$P_n(k_4\le X \le n)=\sum_{i=k_4}^{n} C_n^i \cdot p^i \cdot q^{n-i}$$
• Событие произойдет хотя бы один раз:
  =1-БИНОМ.РАСП(0;n;p;0)
  $$P_n( X \ge 1)=1-P_n(0)=1-q^{n}$$
• Наивероятнейшее число наступлений события $m$:
  =ОКРУГЛВВЕРХ(n*p-q;0)
  $$np-q \le m \le np+p$$

Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) - так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.

Полезное: расчетный файл по формуле Бернулли

Примеры решений задач

Рассмотрим решение типовых задач.

Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.

Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:

$$P_7(5)=C_{7}^5 \cdot 0,75^5 \cdot 0,25^2 = 21\cdot 0,75^5 \cdot 0,25^2= 0,31146.$$

Для вероятности 6 или 7 попаданий суммируем:

$$P_7(6)+P_7(7)=C_{7}^6 \cdot 0,75^6 \cdot 0,25^1+C_{7}^7 \cdot 0,75^7 \cdot 0,25^0= \\ = 7\cdot 0,75^6 \cdot 0,25+0,75^7=0,44495.$$

А вот это решение в файле эксель:

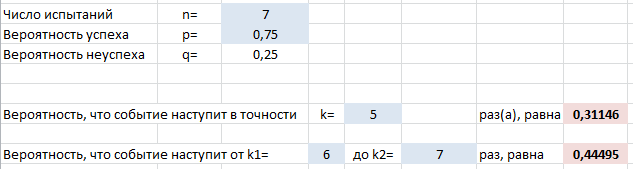
Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?

Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_{10}(k)=C_{10}^k \cdot 0,5^k\cdot 0,5^{10-k}=C_{10}^k \cdot 0,5^{10}$$ Приступим к вычислениям:

$$1. P_{10}(2)=C_{10}^2 \cdot 0,5^{10} = \frac{10!}{2!8!}\cdot 0,5^{10} \approx 0,044.$$ $$2. P_{10}(4)+P_{10}(5)=C_{10}^4 \cdot 0,5^{10} + C_{10}^5 \cdot 0,5^{10}=\left( \frac{10!}{4!6!} + \frac{10!}{5!5!} \right)\cdot 0,5^{10} \approx 0,451.$$ $$3. P_{10}(0)+P_{10}(1)+P_{10}(2)=C_{10}^0 \cdot 0,5^{10} + C_{10}^1 \cdot 0,5^{10}+ C_{10}^2 \cdot 0,5^{10}=\left( 1+10+ \frac{10!}{2!8!} \right)\cdot 0,5^{10} \approx 0,055.$$ $$4. P_{10}(7)+P_{10}(8)+P_{10}(9)+P_{10}(10)=\\ = C_{10}^7 \cdot 0,5^{10} + C_{10}^8 \cdot 0,5^{10}+ C_{10}^9 \cdot 0,5^{10}+ C_{10}^10 \cdot 0,5^{10} =\\=\left(\frac{10!}{3!7!}+ \frac{10!}{2!8!} + 10 +1\right)\cdot 0,5^{10} \approx 0,172.$$ $$5. P_{10}(\ge 1)=1-P_{10}(0)=1-C_{10}^0 \cdot 0,5^{10} = 1- 0,5^{10} \approx 0,999.$$

Наивероятнейшее число мальчиков найдем из неравенства:

$$10 \cdot 0,5 - 0,5 \le m \le 10 \cdot 0,5 + 0,5, \\ 4,5 \le m \le 5,5,\\ m=5.$$

Наивероятнейшее число - это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).

Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

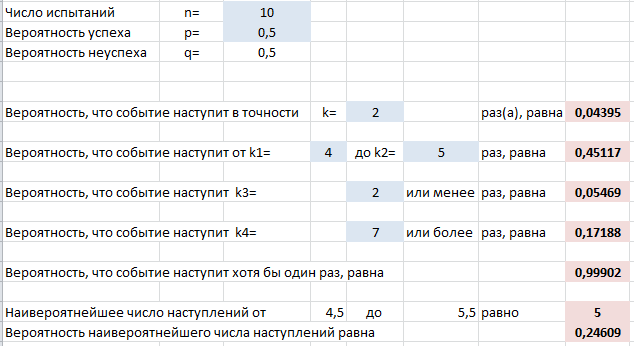
Видно, что ответы совпадают.

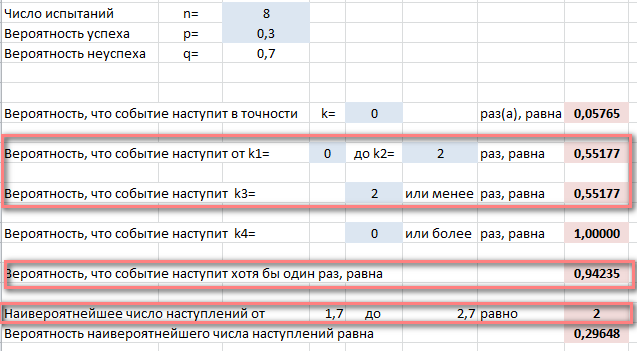
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?

Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!

Полезные ссылки

Расчетный файл эксель для расчетов по формуле Бернулли

Калькуляторы на формулу Бернулли Примеры решений задач

Формулы Лапласа и Пуассона в Эксель Решение заданий на заказ

Решебник задач по вероятности