Комбинаторика в Excel

Давайте разберем на примерах основные формулы комбинаторики: сочетания, размещения, перестановки без повторений и научимся вычислять их с помощью встроенных функций Excel.

Ниже вы найдете для каждой формулы инструкции по вычислению в эксель, пример задачи, ссылку на калькулятор и видеоурок и шаблон Excel. Удачи в изучении!

Как выбрать формулу комбинаторики?

Нужно последовательно (см. схему выше) ответить на несколько вопросов:

• Сколько у нас есть объектов (число $n$)?
• Важен ли их порядок в комбинации?
• Могут ли встречаться повторяющиеся элементы?
• Нужно выбрать все элементы или только $k\lt n$?

Отвечая на эти вопросы, двигаемся по стрелкам схемы и получаем название формулы комбинаторики:

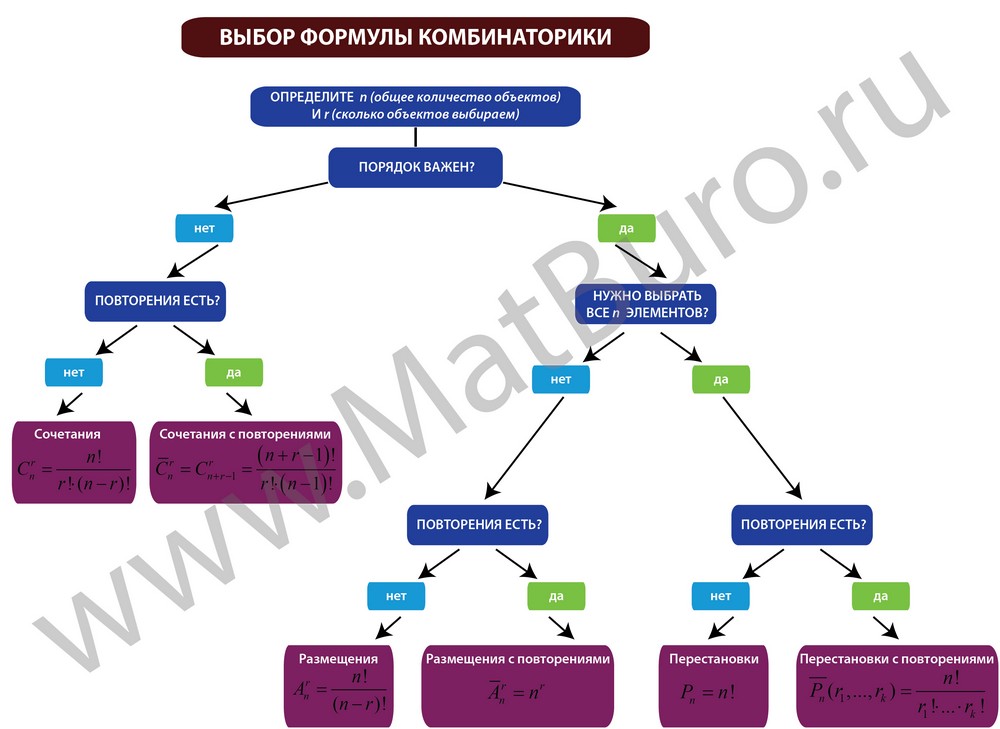
Схема выбора формул с примерами задач

Перестановки в Excel

Пусть имеется $n$ различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

$$P_n=n!=1\cdot 2\cdot 3 \cdot ... \cdot (n-1) \cdot n$$

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.

Подробнее: факториал в эксель.

Для нахождения числа перестановок в Excel можно использовать одну из двух функций:

=ПЕРЕСТ($n$;$n$) или =ФАКТР($n$), где $n$ - число переставляемых объектов.

Задача. Сколькими способами можно расставить 10 различных книг на одной полке?

Вводим число объектов 10 и получаем ответ: 3628800 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор перестановок.

Перестановки с повторениями в Excel

Пусть имеется $n$ объектов различных типов: $n_1$ объектов первого типа, $n_2$ объектов второго типа,... $n_k$ объектов $k$-го типа. Сколькими способами можно переставить все объекты между собой?

Будем переставлять $n$ объектов всеми возможными способами (их будет $n!$). Но так как некоторые объекты совпадают, итоговое число будет меньше. В частности, $n_1$ объектов первого типа можно переставлять между собой $n_1!$ способами, но они не меняют итоговую перестановку. Аналогично для всех остальных объектов, поэтому число перестановок с повторениями есть

$$P_n (n_1,n_2,...,n_k)=\frac{n!}{n_1! \cdot n_2!\cdot ... \cdot n_k!}.$$

Для нахождения числа перестановок в Excel будем использовать функцию =ФАКТР(), которая находит факториал чисел и обычные действия (умножение, деление).

Задача. Сколько различных слов можно составить из букв слова "колокол"?

Вводим число букв $n=7$, а также $n_1=2$ (2 буквы "к"), $n_2=3$ (3 буквы "о"), $n_3=2$ (2 буквы "л"), и получаем ответ: 210 слов.

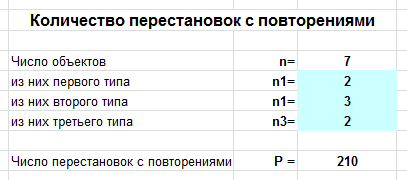
В режиме формул это выглядит так:

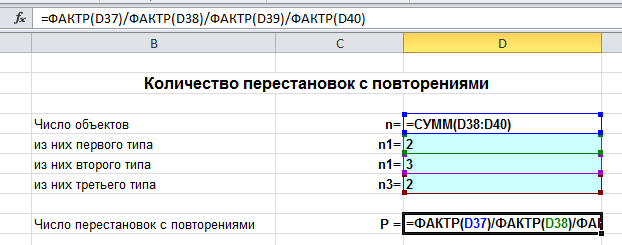
Еще: онлайн калькулятор перестановок c повторениями.

Размещения в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $k$, а их число равно

$$A_n^k=\frac{n!}{(n-k)!}=n\cdot (n-1)\cdot ... \cdot (n-k+1)$$

Для нахождения числа размещений в Excel используем функцию =ПЕРЕСТ($n$;$k$).

Задача. В группе учится 10 студентов. Нужно выбрать из них 3 человек на должности старосты, заместителя и дежурного. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 720 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений.

Размещения с повторениями в Excel

Число размещений с повторениями из $n$ объектов по $k$ можно найти по формуле

$$\overline{A}_n^k=n\cdot n\cdot ... \cdot n = n^k.$$

Для вычисления в Excel используем функцию =СТЕПЕНЬ($n$;$k$).

Задача. Сколько трехзначных номеров можно составить для автомобилей, используя все возможные цифры от 0 до 9?

Вводим $n=10$ (количество возможных цифр), $k=3$ (количество цифр в номере) и получаем ответ: 1000 номеров.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений с повторениями.

Сочетания в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $k$, а их число равно

$$C_n^k=\frac{n!}{(n-k)!\cdot k!}$$

Для нахождения числа сочетаний в Excel используем функцию =ЧИСЛКОМБ($n$;$k$).

Задача. В поход пошло 10 учеников. Нужно выбрать из них 3, которые понесут флажки. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 120 способов.

В режиме формул это выглядит так:

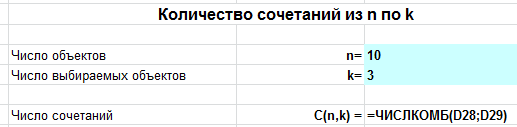
Еще: онлайн калькулятор сочетаний.

Сочетания с повторениями в Excel

Количество сочетаний с повторениями из $n$ объектов по $k$ можно найти по формуле

$$\overline{C}_n^k=C_{k+n-1}^k=\frac{(k+n-1)!}{(n-1)!\cdot k!}$$

Для вычисления в Excel используем функцию =ЧИСЛКОМБ($n+k-1$;$k$).

Задача. В магазине продаются мячики трех цветов: желтые, красные и синие. Родительский комитет собирается купить 10 мячиков. Сколько возможных вариантов выбора у них есть?

Вводим $n=3$ (вида объектов), $k=10$ (нужно выбрать) и получаем ответ: 66 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор сочетаний с повторениями.

Полезные ссылки

Для собственных расчетов скачайте файл: Комбинаторика в Excel.

Онлайн калькуляторы Онлайн учебник: Элементы комбинаторики Примеры решений

Как решать задачи по комбинаторике? Видеоуроки по комбинаторике Решение на заказ

Решебник задач по комбинаторике